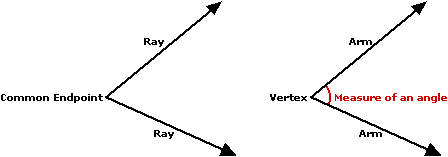
জ্যামিতিতে, কোণ বলতে বোঝায় দুটি রশ্মি (বা দুইটি রেখাংশ)-এর সাধারণ শীর্ষবিন্দুতে মিলিয়ে যে আদ্দিক ফাঁকা স্থান তৈরি হয়। (Edudesh) সহজভাবে বললে, দুটি রেখা বা রশ্মি এক বিন্দুতে মিলিত হয়ে যার মধ্যবর্তী অংশ তার কোণ। (Edudesh)
এই ধারণাটি শিক্ষার্থীদের জন্য মৌলিক হলেও, বিভিন্ন প্রকারভেদ ও অবস্থার কারণে “কোণ কাকে বলে”-এর পরিসর বেশ বিস্তৃত। আজ আমরা সেটি বিস্তারিতভাবে বিশ্লেষণ করব—চিত্রসহ, উদাহরণসহ, এবং প্র্যাকটিক্যাল প্রয়োগসহ।
১. কোণ কাকে বলে – সংজ্ঞা ও মূল উপাদান
সংজ্ঞা
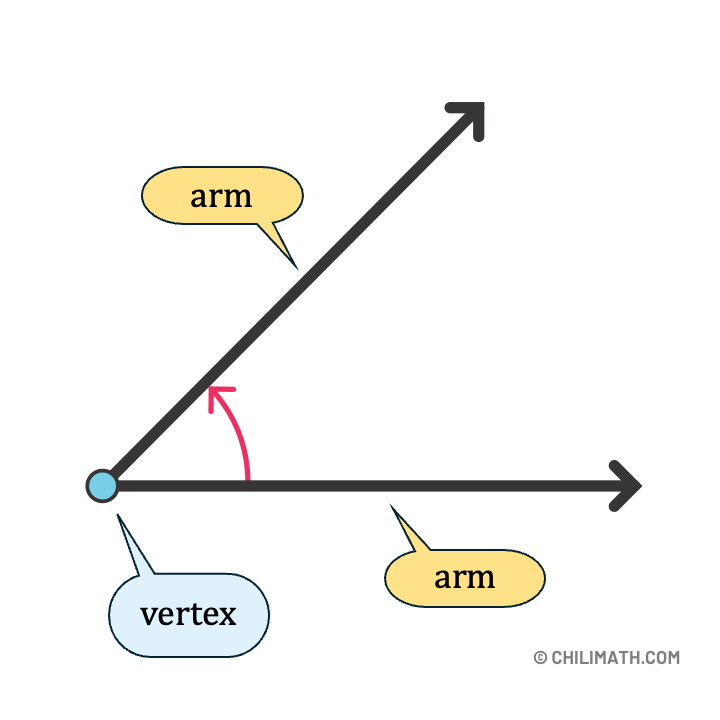
- “সমতলস্থ দুইটি রশ্মি যদি এক সাধারণ প্রান্তবিন্দুতে মিলিত হয়, এবং তাদের বাহু একই না হয়, তাহলে সেই মিলিত বিন্দুতে উৎপন্ন স্থানকে কোণ বলা হয়।” (Edudesh)
- এক ভিন্ন ভাষায়: দুইটি রেখাংশ বা রশ্মি পরস্পর মিলিত হলে যে জ্যামিতিক বিন্দুটি উৎপন্ন হয় তা কোণ। (1TimeSchool.Com – Education for All)
মূল উপাদান
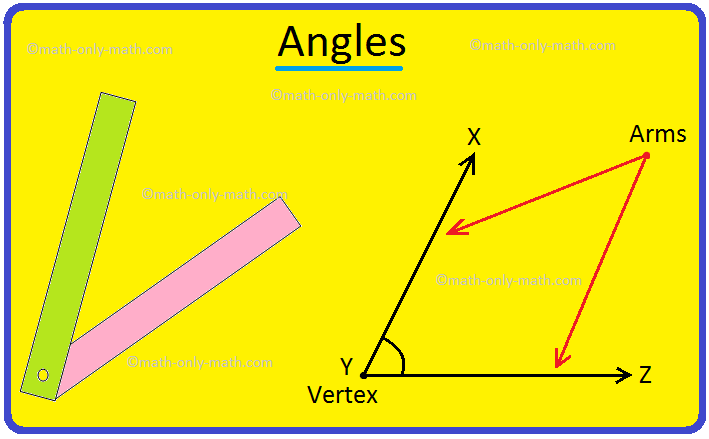
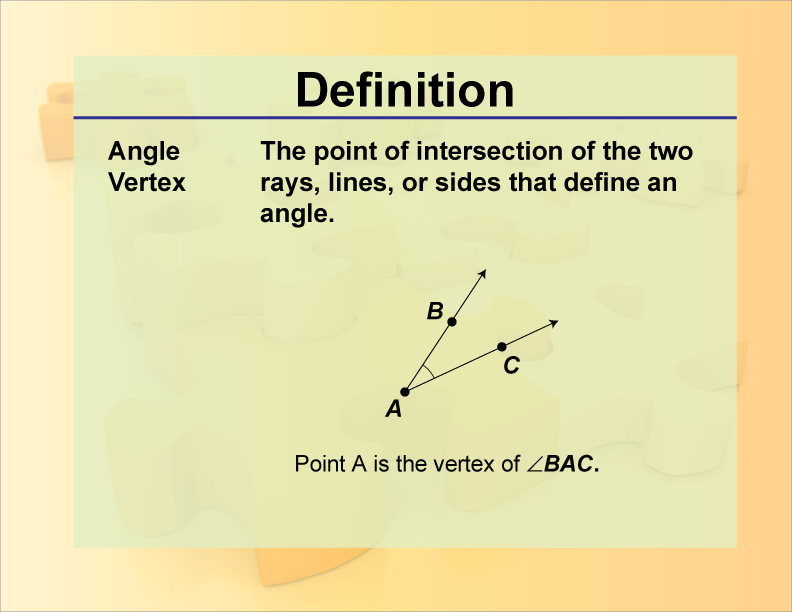
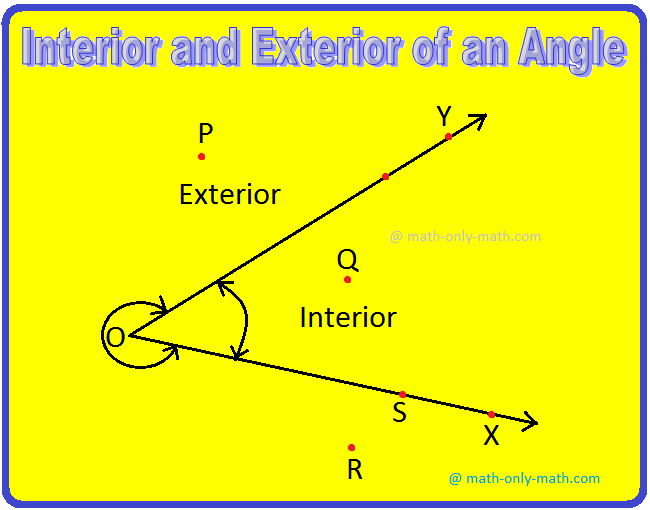
- শীর্ষবিন্দু (Vertex): রশ্মি দুটি যেখানে মিলিত হয়।
- বাহু (Arms): দুটি রশ্মি বা রেখাংশ।
- ভিতরের অংশ / অভ্যন্তর (Interior) ও বহির্ভাগ (Exterior): কোণের ভিতরের ও বাইরের অঞ্চল। (Edudesh)
- কোণের পরিমাপ সাধারণত ডিগ্রি (°) দ্বারা হয়। (1TimeSchool.Com – Education for All)
উদাহরণ
একটি ঘড়ির কাটার ঘোরার পথে যদি দুইটি অবস্থানের মধ্যে হয়, তাহলে সেই ঘোরার পথই দুই কাটার বাহু দ্বারা গঠিত একটি কোণ।
২. কোণ কাকে বলে কত প্রকার ও কি কি
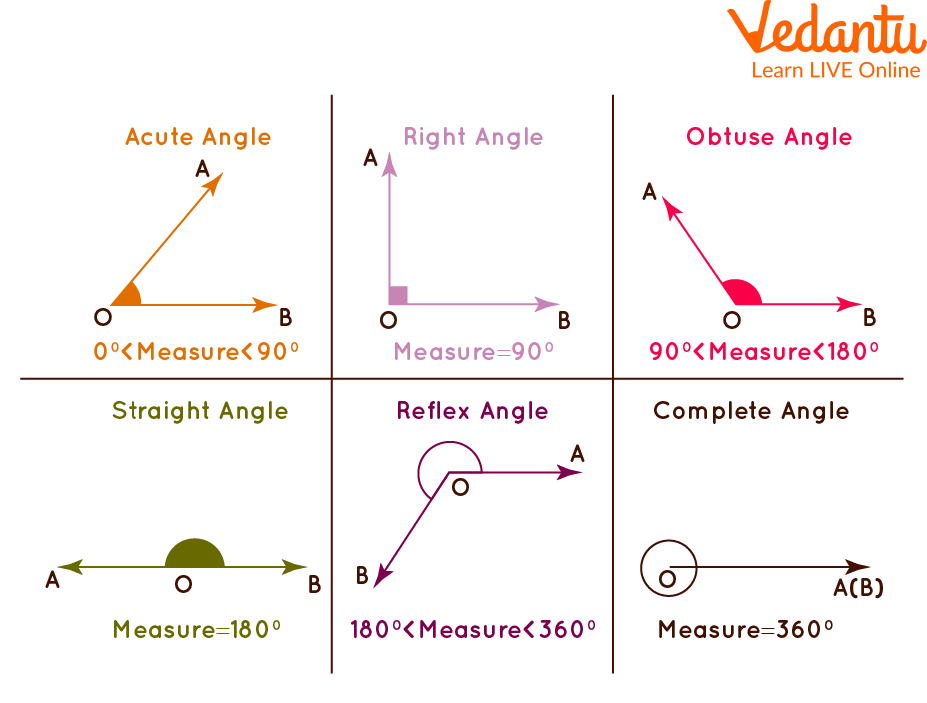
কোণ বিভিন্নভাবে প্রকারভেদ করা হয়। সাধারণভাবে আমরা নিচের মূল ভাগগুলো দেখি:
- শূন্য কোণ (0°)
- সূক্ষ্মকোণ (0° < θ < 90°)
- সমকোণ (θ = 90°)
- স্থূলকোণ (90° < θ < 180°)
- সরলকোণ (θ = 180°)
- প্রবৃদ্ধ কোণ (180° < θ < 360°)
- পূর্ণকোণ (θ = 360°) (Edudesh)
এই মূল ভাগের পাশাপাশি বিশেষ নামসহ কোণগুলো পাওয়া যায়; পরবর্তীতে সেগুলো বিশ্লেষণ করা হবে।
৩. “সন্নিহিত কোণ কাকে বলে”
সংজ্ঞা
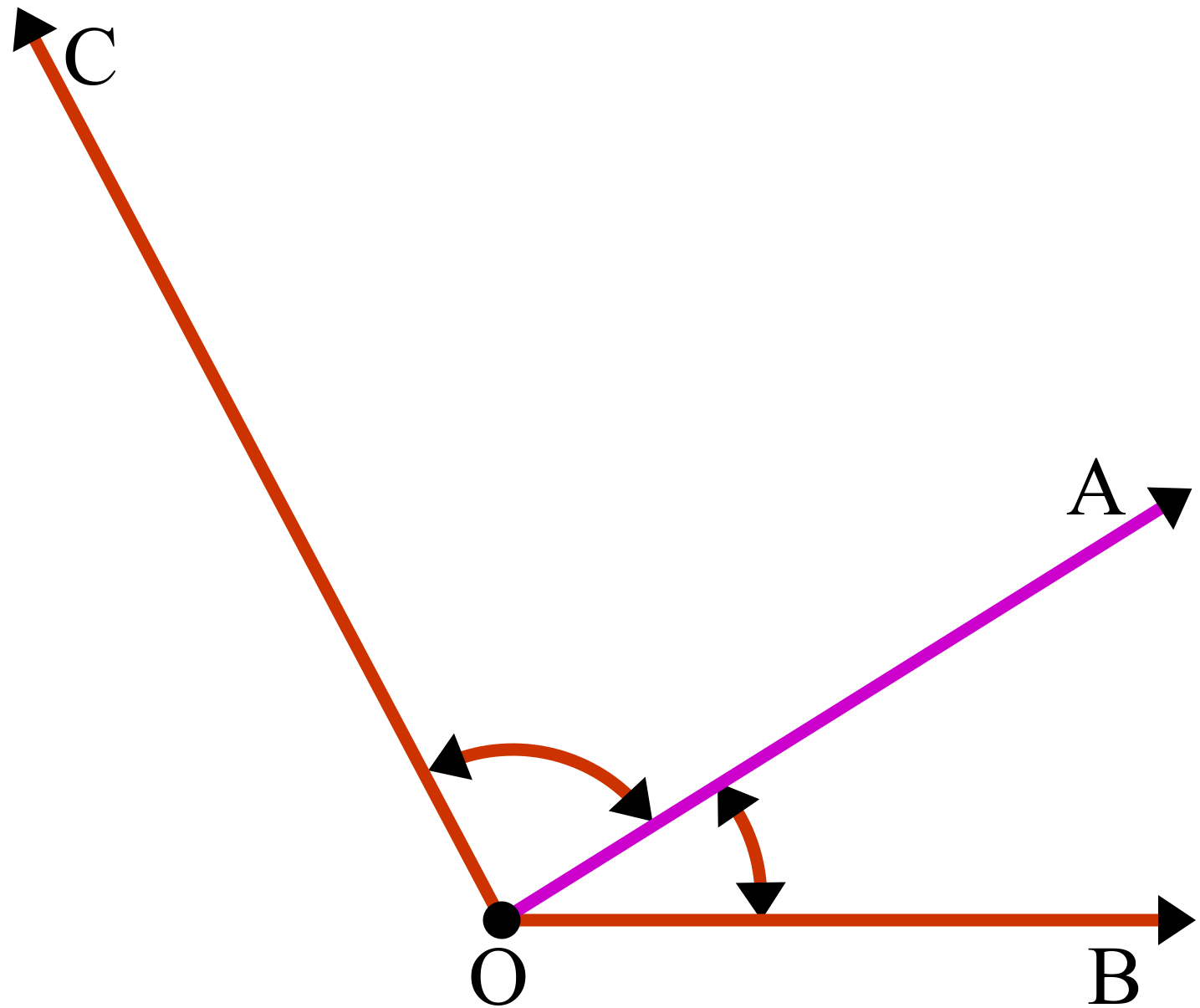
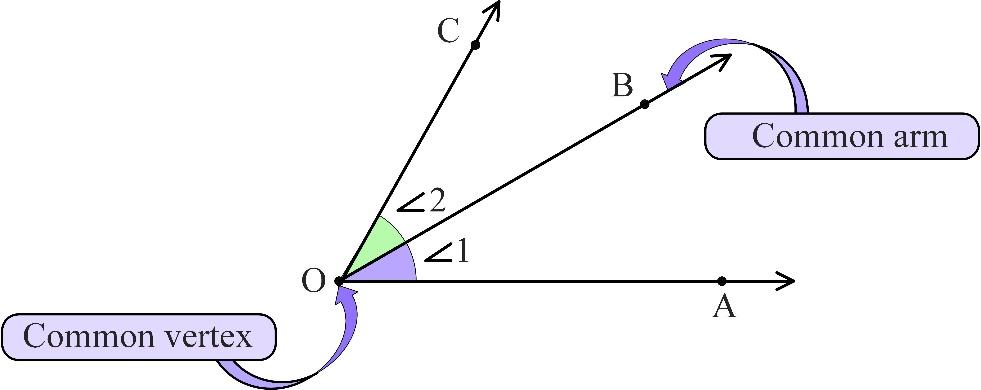
যদি একই শীর্ষবিশিষ্ট দুইটি কোণ থাকে এবং একটি সাধারণ বাহু হয়, এবং আরেক বাহু দুটি বিপরীত দিকে থাকে — তাহলে সেই দুই কোণকে পরস্পর সন্নিহিত কোণ বলা হয়। (Edudesh)
উদাহরণ
ধরা যাক AB ও AC দুইটি রশ্মি O বিন্দুতে মিলেছে। আর OB ও OD রশ্মি মিলেছে O-তে। ∠AOB ও ∠BOC এই দুটি কোণ যদি সাধারণ বাহু OB ভাগ করে আর অন্য বাহুগুলো বিপরীত দিকে থাকে, তাহলে এরা সন্নিহিত কোণ।
বৈশিষ্ট্য
- দুই কোণের শীর্ষ এক।
- এক বাহু সাধারণ।
- অভ্যন্তরস্থ বিন্দু সাধারণ নয়।
৪. “পূরক কোণ কাকে বলে”
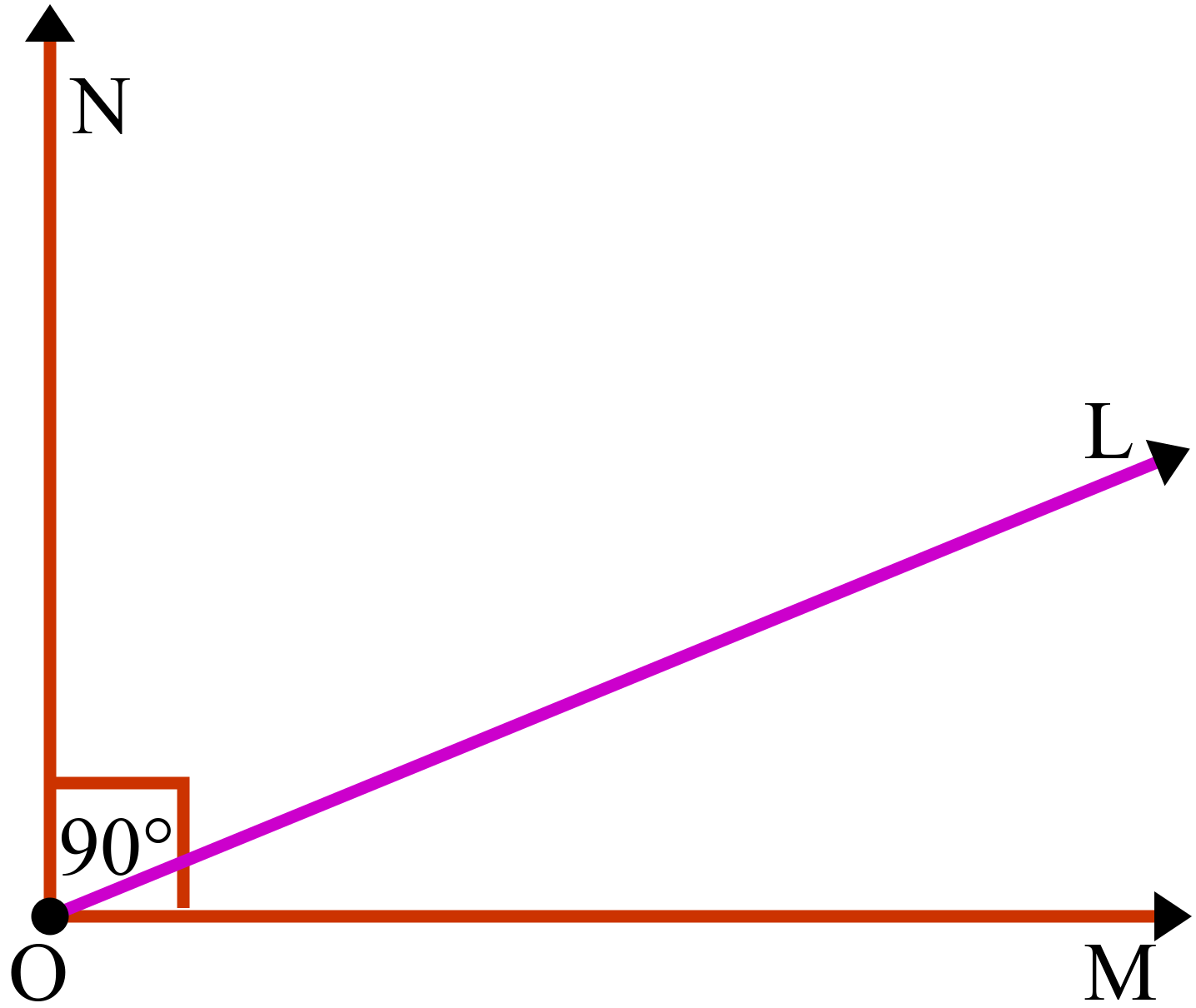
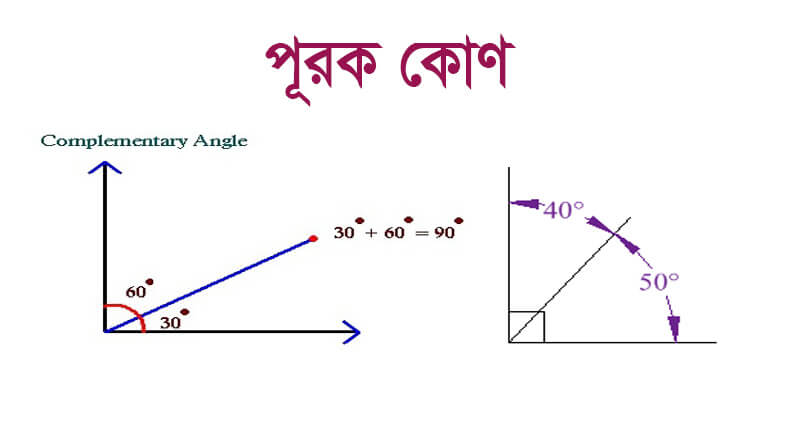
সংজ্ঞা
দুটি কোণের যোগফল যদি ৯০° হয়, তাহলে তাদেরকে পূরক কোণ বলা হয়। (Edudesh)
উদাহরণ
∠A = 30° ও ∠B = 60° হলে ∠A ও ∠B হলো পরস্পর পূরক কোণ।
ব্যবহার
সাধারণত ট্রায়াঙ্গেল বা সমকোণীয় ত্রিভুজের ক্ষেত্রে সূক্ষ্মকোণ দুটি পরস্পর পূরক হয়। (1TimeSchool.Com – Education for All)
পরিবেশ কাকে বলে? (Best Guide 2026)
৫. “সম্পূরক কোণ কাকে বলে”
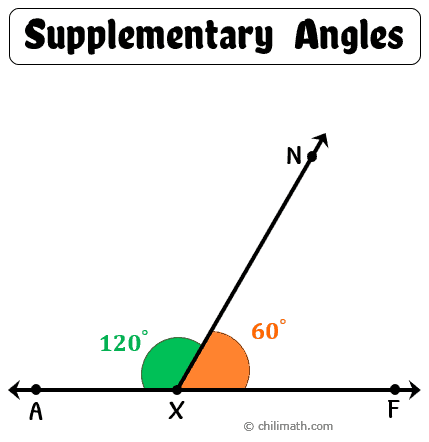
সংজ্ঞা
দুটি কোণের যোগফল যদি ১৮০° হয়, তাহলে তাদেরকে সম্পূরক কোণ বলা হয়। (TonBangla)
উদাহরণ
∠X = 110° ও ∠Y = 70° হলে ∠X ও ∠Y হলো পরস্পর সম্পূরক কোণ।
বিশ্লেষণ
- যদি এই দুই কোণ সন্নিহিত হয় (একই শীর্ষ-বিন্দু ও সাধারণ বাহু) তাহলে তাদের বাহুগুলো একটি সরলরেখায় অবস্থান করবে। (1TimeSchool.Com – Education for All)
- অন্যভাবে, সম্পূরক কোণ দুটি এক লাইনে হতে হবে এমন কোনো বাধ্যকর নিয়ম নেই — শুধু যোগফল ১৮০° বিষয়টি। (Edudesh)
৬. “বিপ্রতীপ কোণ কাকে বলে”
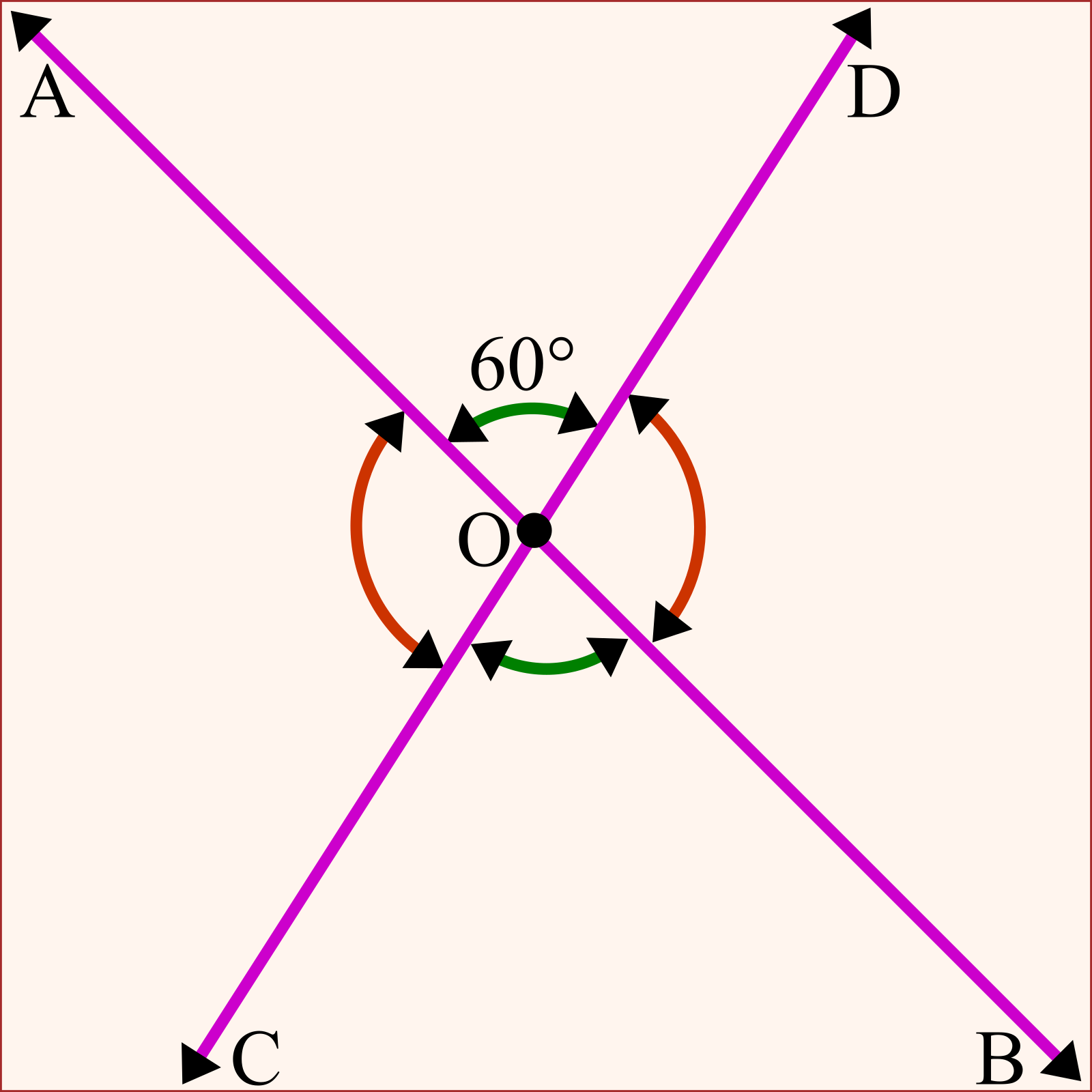
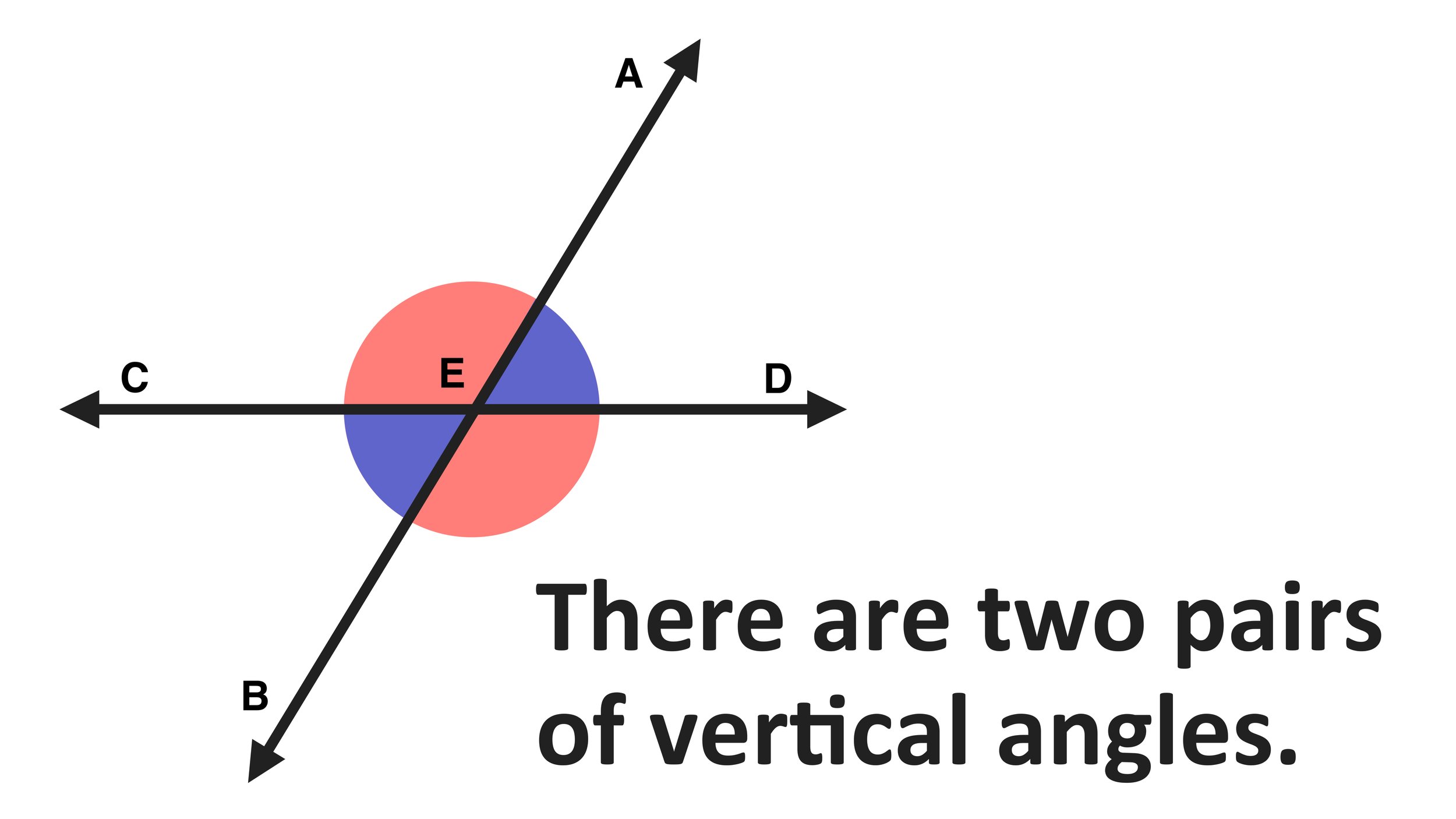
সংজ্ঞা
যখন দুইটি সরলরেখা এক বিন্দুতে ছেদ হয়, তখন দুইটি কোণ বিপরীত অবস্থানে তৈরি হয়। সেই দুইটোকে বিপ্রতীপ কোণ বলা হয়। (Edudesh)
উদাহরণ
AB এবং CD রেখা O বিন্দুতে ছেদ করলো। সেখানে উৎপন্ন কোণগুলোর মধ্যে ∠AOD ও ∠BOC যেসব বাহুর বিপরীত রশ্মি দ্বারা হয়, সেগুলো পরস্পর বিপ্রতীপ। এবং তারা সমান হয়। (Edudesh)
৭. “একান্তর কোণ কাকে বলে”
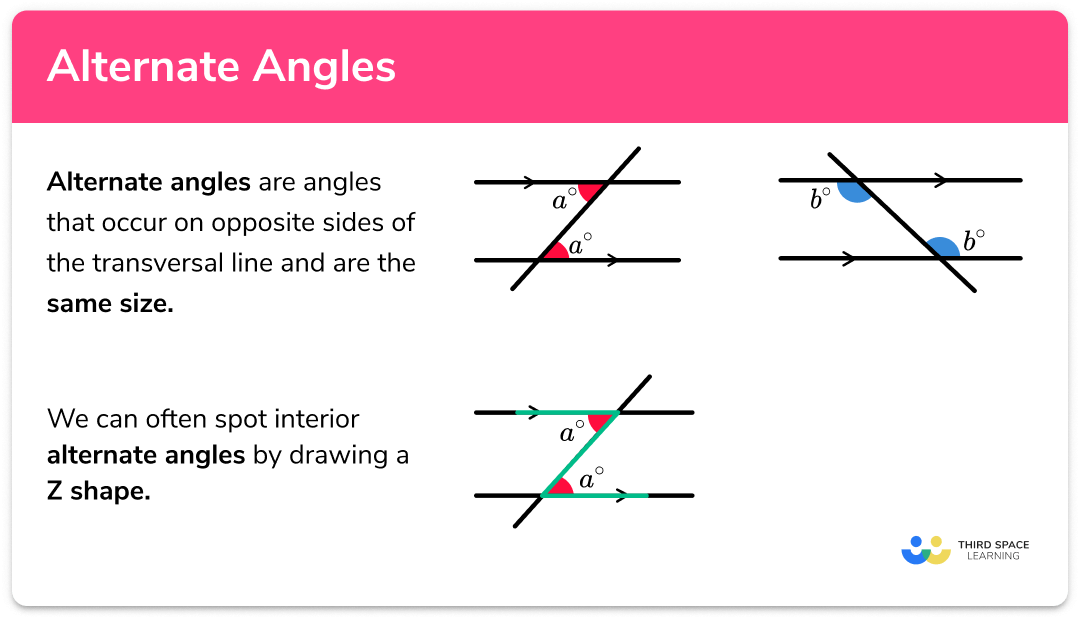
সংজ্ঞা
যখন দুইটি সমান্তরাল রেখাকে (Parallel lines) একটি ছেদক (Transversal) ছেদ করে, তখন যে দুইটি কোণ তৈরি হয় যাদের শীর্ষবিন্দু ভিন্ন, এবং তারা ছেদকের বিপরীত পাশে অবস্থান করে, এবং উভয়েই অন্তঃস্থ (interior) অথবা উভয়েই বহিঃস্থ (exterior) হয়— সেই কোণদ্বয়কে একান্তর কোণ বলা হয়। (Edudesh)
উদাহরণ
লেখচিত্রে ল1 ও ল2 সমান্তরাল রেখা। ছেদক ল3। আপনি দেখা পাবেন ∠৫ ও ∠৭ হলো একান্তর কোণ।
বৈশিষ্ট্য
- তারা সমান হয়, যদি রেখাদ্বয় সমান্তরাল হয়।
- সমান্তরাল রেখার প্রমাণে একান্তর কোণ খুব ব্যবহার হয়।
৮. অন্যান্য বিশেষ কোণ ও শ্রেণিবিভাগ
নিচে অন্যান্য কিছু বিশেষ কোণ ও সংক্ষিপ্ত পরিচয় দেওয়া হলো:
| কোণ | সংক্ষেপে পরিচয় |
|---|---|
| কেন্দ্রস্থ কোণ (Central Angle) | একটি বৃত্তে কেন্দ্রে উৎপন্ন কোণ। |
| বৃত্তস্থ কোণ (Inscribed Angle) | একটি বৃত্তে ব্যাসরেখার উপর অংকিত কোণ। |
| বহিঃস্থ কোণ (Exterior Angle) | বহুভুজের বাহু বর্ধিত করলে যে কোণ উৎপন্ন হয়। |
| উন্নতি কোণ ও অবনতি কোণ | সাধারণভাবে ত্রিভুজে ভূমি-রেখা তুলনায় উৎপন্ন বিশেষ কোণ। (1TimeSchool.Com – Education for All) |
| রেফারেন্স কোণ, রেডিয়ান কোণ, কোটা-টার্মিনাল কোণ | উচ্চতর অংকে ব্যবহৃত কোণ মডেল। |
প্রয়োজনে প্রতিটি কোণের জন্য চিত্রসহ পরবর্তী ধাপে প্রয়োজনে এক করে আলোচনা করা যেতে পারে।
৯. কোণ কাকে বলে – প্র্যাকটিক্যাল উদাহরণ ও প্রয়োগ
- একটি ত্রিভুজের তিন কোণের সমষ্টি সবসময় ১৮০° হয়। (1TimeSchool.Com – Education for All)
- একটি বহুভুজের অন্তঃস্থ ও বহিঃস্থ কোণের সমষ্টি দুই সমকোণ (১৮০°) হয়। (Edudesh)
- স্থাপত্য, প্রকৌশল, ডিজাইন-এ কোণের প্রকৃতি বুঝতে পারা জরুরি।
- দৈনন্দিন জীবনে ঘড়ির কাঁটা, দরজার ভাঁজ, ছাদের কোণা—সবকিছুর মধ্যে কোণ দেখা যায়।
১০. Frequently Asked Questions (FAQs)
Q1: কোণ কাকে বলে সংক্ষিপ্তভাবে?
A: কোণ হল দুইটি রশ্মি বা রেখাংশের মিলন-বিন্দুতে উৎপন্ন সেই জ্যামিতিক স্থান।
Q2: সন্নিহিত কোণ ও একান্তর কোণের পার্থক্য কি?
A: সন্নিহিত কোণে এক শীর্ষ ও সাধারণ বাহু থাকে; একান্তর কোণে দুইটি ভিন্ন শীর্ষবিন্দু এবং সাধারণ নয় বাহু হয়।
Q3: পূরক ও সম্পূরক কোণের মধ্যে কি ভেদ আছে?
A: হ্যাঁ, পূরক কোণে দুই কোণের যোগফল হয় ৯০°; সম্পূরক কোণে হয় ১৮০°।
Q4: বিপ্রতীপ কোণ সবসময় সমান হয় কি?
A: হ্যাঁ, দুই সরলরেখার ছেদে উৎপন্ন বিপরীত কোণ-দ্বয় সমান হয়।
Q5: রেডিয়ান কোণ কি এবং কোণ কাকে বলে তার সঙ্গে কি সম্পর্ক?
A: রেডিয়ান হলো কোণের পরিমাপের আরেক একক; “কোণ কাকে বলে” শিরোনামের আলোচনায় মূলত ডিগ্রি-ভিত্তিক হলেও রেডিয়ান ধারনাটি উচ্চতর অংকে গুরুত্বপূর্ণ।
১১. উপসংহার
আজ আমরা বিশ্লেষণ করেছি “কোণ কাকে বলে”-এর সংজ্ঞা, প্রকারভেদ, বৈশিষ্ট্য ও বিভিন্ন বিশেষ কোণ-রূপ—সহ চিত্রযুক্ত উদাহরণ। এই ধারণাগুলো ভালোভাবে বোঝা হলে, জ্যামিতি, ত্রিকোণমিতি ও ডিজাইন-সহ অন্য যে কোনো বিষয় সহজ হবে।
আপনি কি কোনো নির্দিষ্ট কোণ (যেমন একান্তর কোণ, বৃত্তস্থ কোণ বা রেডিয়ান কোণ) নিয়ে আরও চিত্রসহ আলোচনা চান? মন্তব্যে জানান—আমি সেগুলোও অন্তর্ভুক্ত করতে পারি। পড়ার জন্য ধন্যবাদ!
